Here’s an explanation of in-class flip with its types of stations, sequencing and examples based on trial and error (still in process).
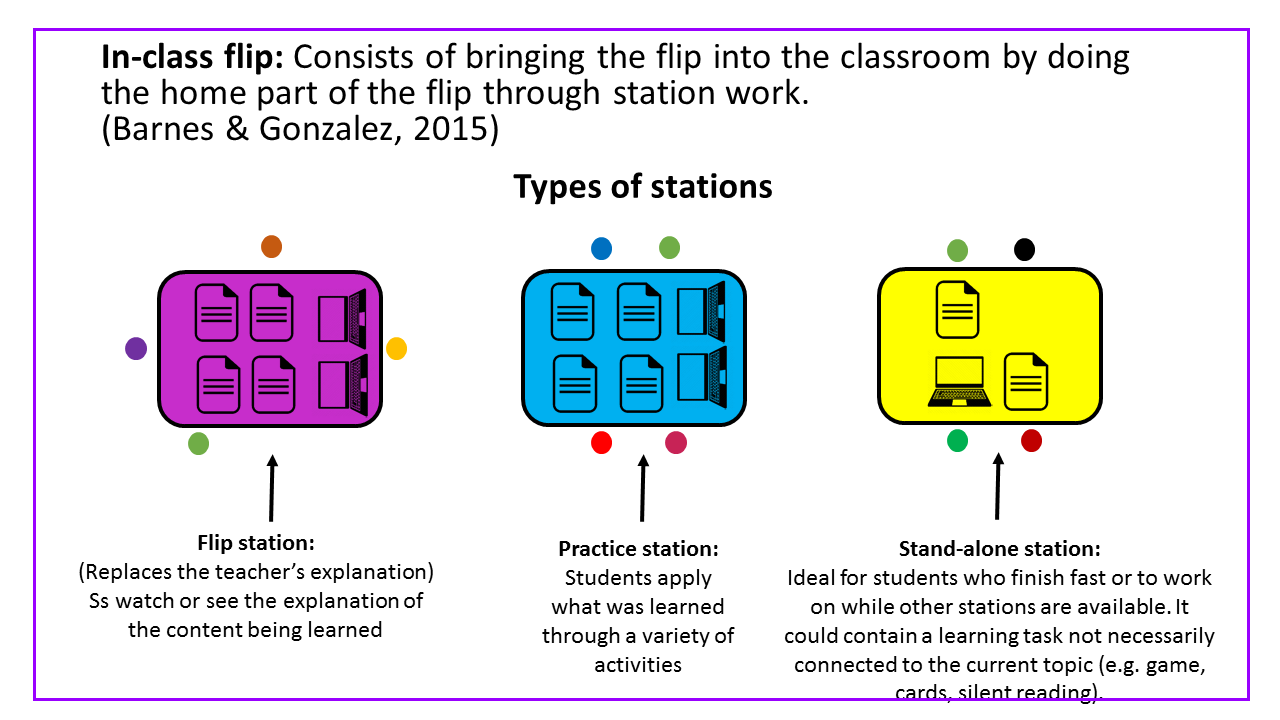
What is in-class flip?
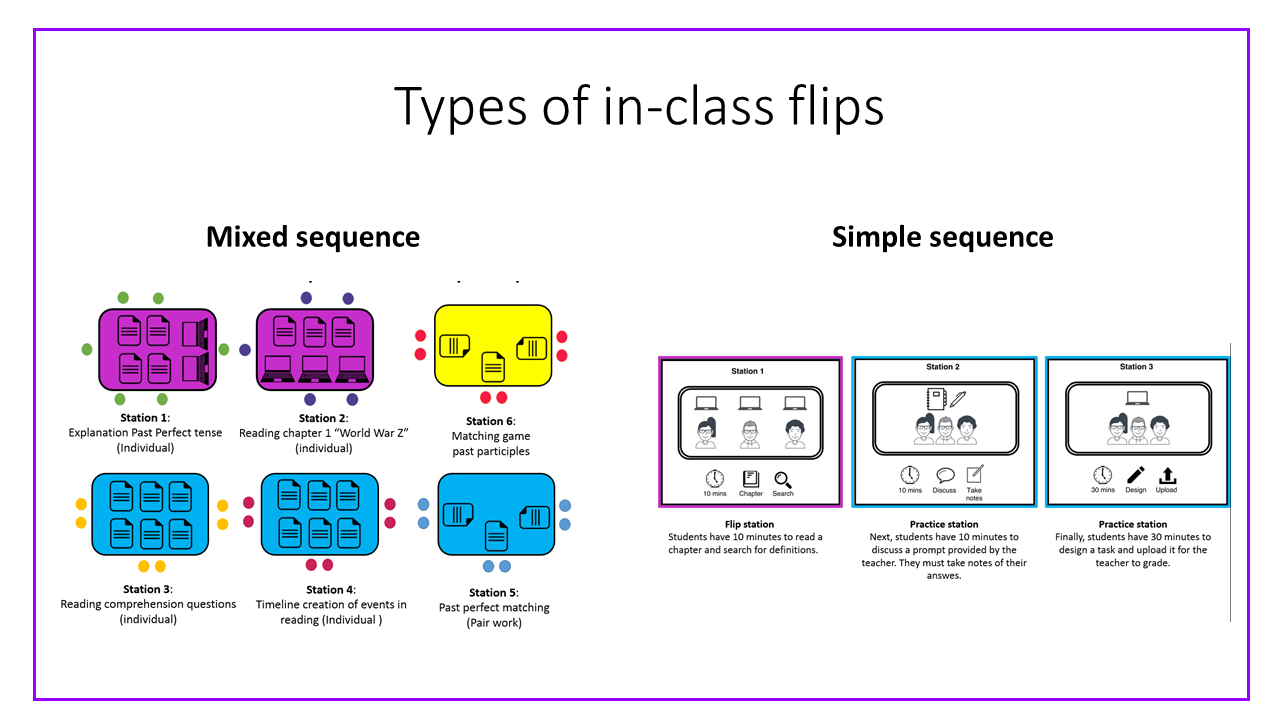
Types of in-class flips
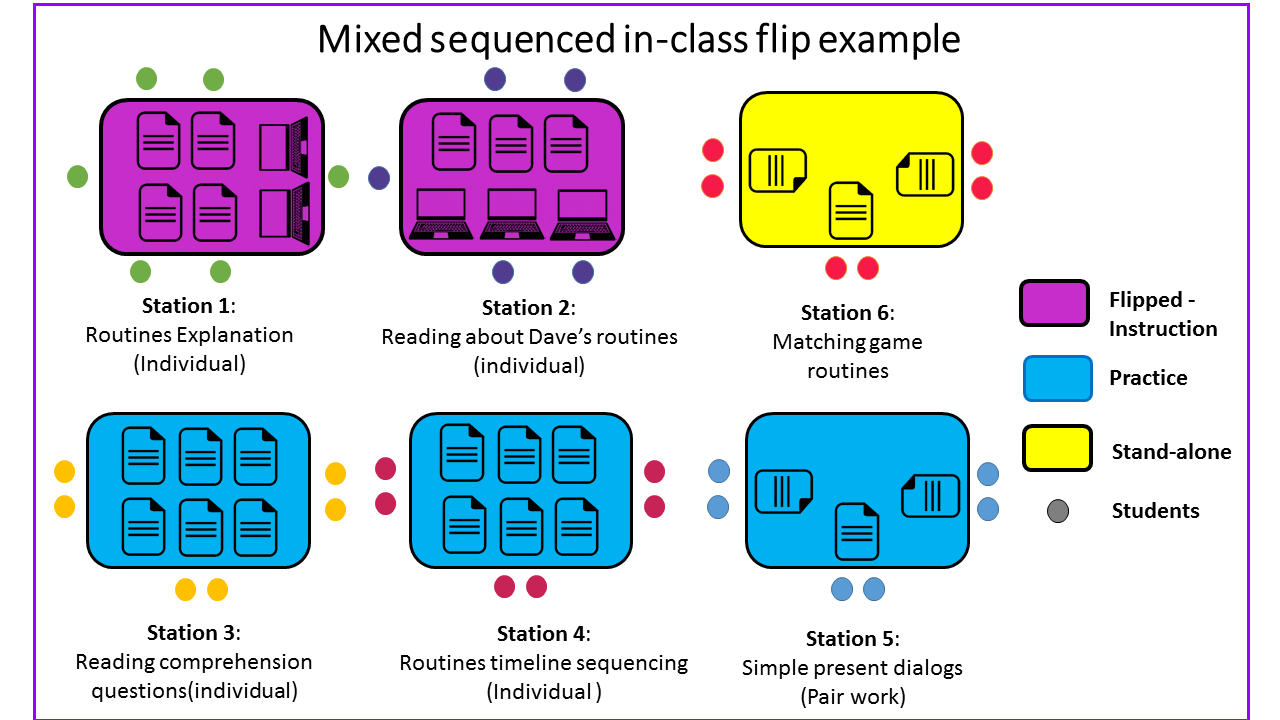
Mixed sequence stations explanation

Mixed sequenced in-class flip example
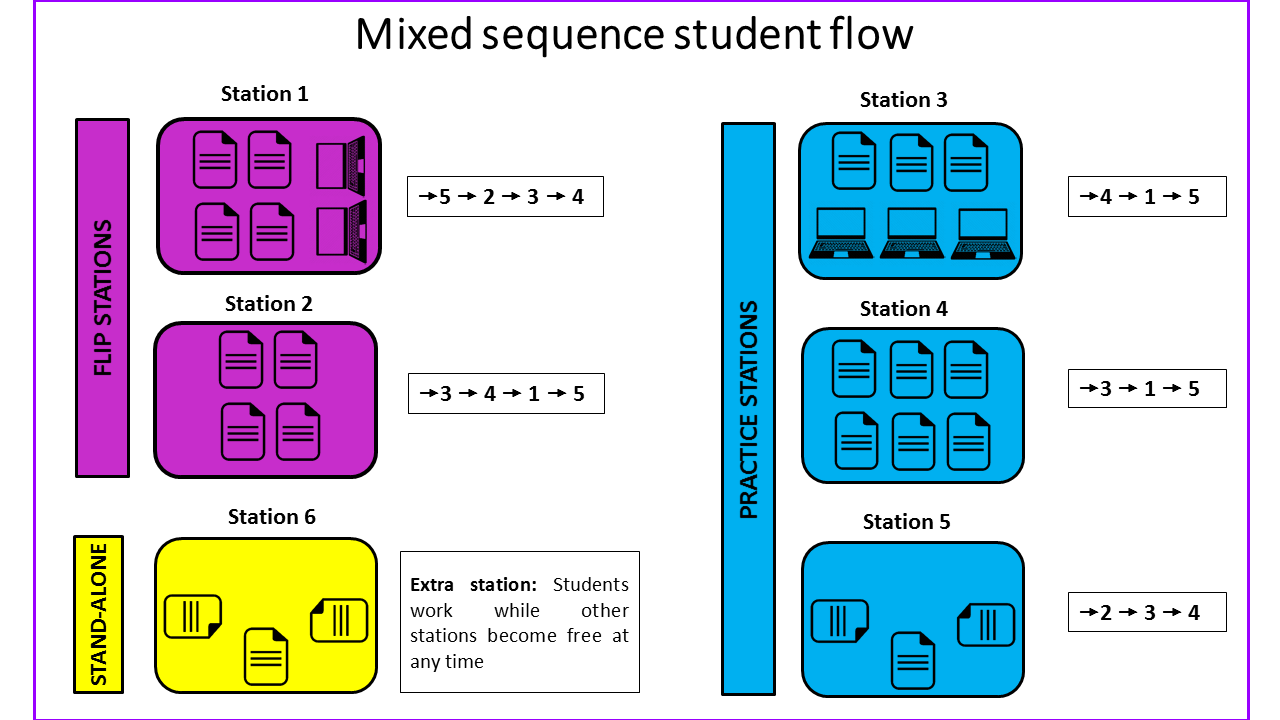
Mixed sequence student flow
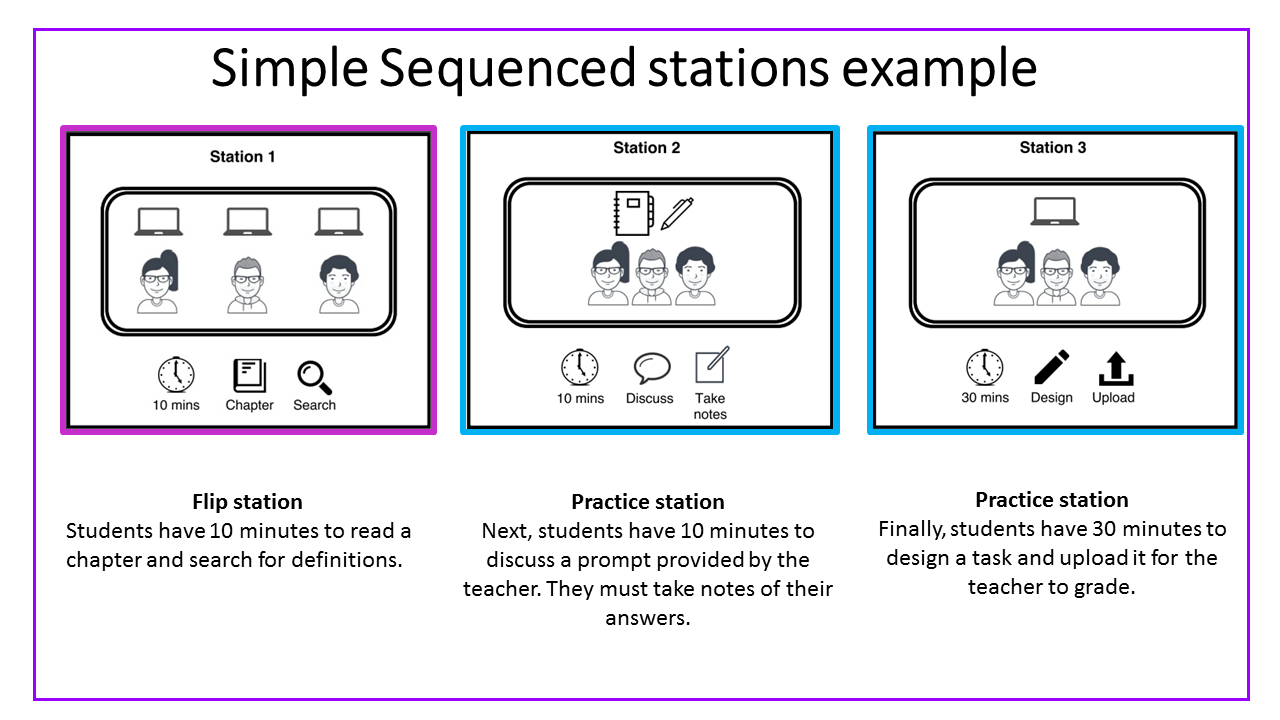
Simple sequence stations explanation

Simple sequenced stations example
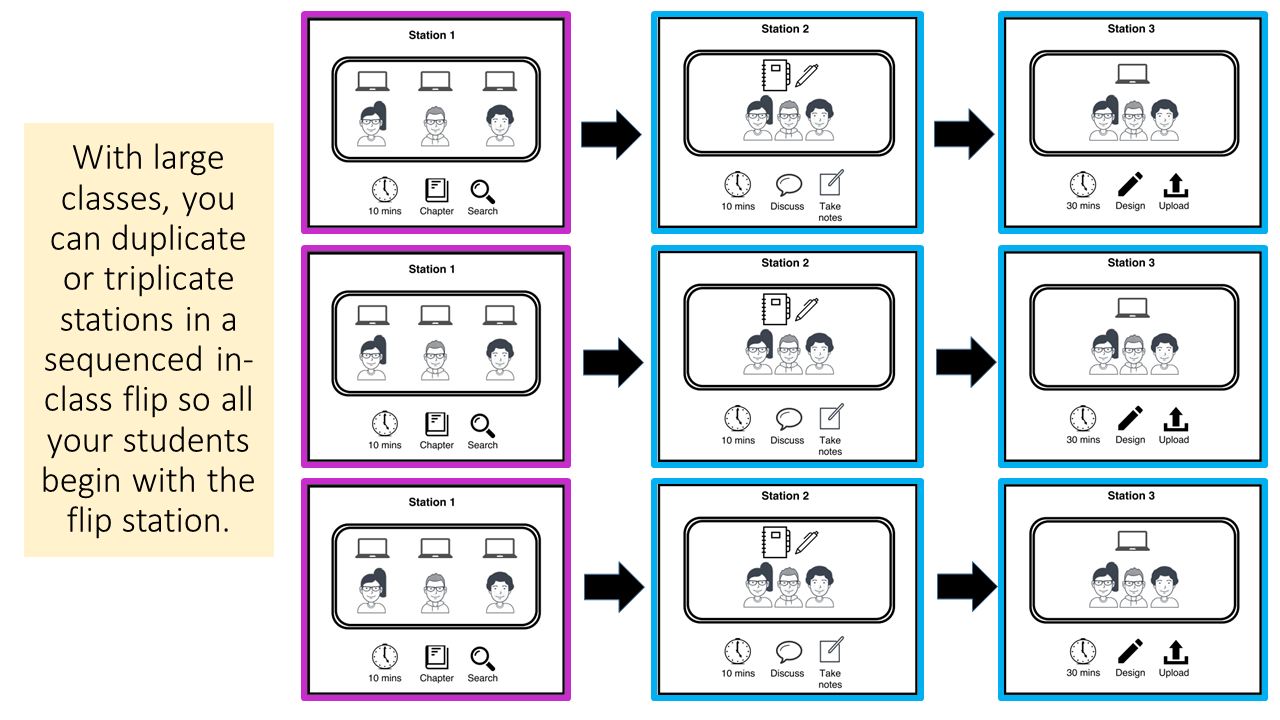
What to do with large classes (In a sequenced flip)
Some ideas for station work

It is important to note that every in-class flip will vary depending on number of students, physical class space, resources, class focus and student dynamic, among other aspects. Sequenced or mixed flips depend on every teachers needs and individual class needs as well. Getting one’s head around the logistics is a process, but once you get the hang of it, you’ll love it!
Feel free to leave your comments and questions!
References:
Barnes, M., & Gonzalez, J. (2015). Hacking Education: 10 Quick Fixes for Every School (Hack Learning Series). Cleveland, OH: Times 10 Publication.
González, J. (2014) Modifying the Flipped Classroom: The “In-Class” Version. Retrieved from http://www.edutopia.org/blog/flipped-classroom-in-class-version-jennifer-gonzalez
Icons taken from draw.io
Martha: this is a great representation of the “In-Flip.” I really like the images and the explanations. This will be a very helpful tool for many teachers as they make the transition to flipped learning.
Jon: absolutely! Thanks for your comments. That’s the idea, to show and share with teachers ways they can flip according to their needs and contexts. More posts to come! 🙂
Hi Martha, the approach proves to provide classes with innovation, I like that it fosters metacognitive strategies such as self-monitoring, and assessing. I just wonder what are the most frequent types of tasks your students produce, for instance in a pronunciation class?
Great question!A variety of tasks can be used depending on the approach you are taking for teaching pronunciation. Witihn a communicative framework, like the one proposed by Celce-Murcia, Brinton and Goodwin (2010), you will have listening descrimination tasks, which will require the student to demonstrate they can differentiate the pronunciation feature you are teaching, then come the controlled tasks which are any activity that will provide strict practice of the feature, like reading aloud, tongue twisters, etc. Next, you have the guided exercises which are the Student A, Student B type exercises, dialogs or communciation games that allow students to start communicating with each other following a model. Finally, the communicative activities, such as discussions, interviews, etc., where students can demonstrate they can apply the pronunciation feature in a communicative way without a model. Thanks for your comment. 🙂
Hi Martha, just wondering how do you manage with the feedback? How students are checking their answers? Are you giving them an answer key?
At what stage do they have acess to the answer key?
Also, I was just wondering. It looks like these type of stations work will only work with worksheets (that you place in each station) What about if students follow a coursebook and the practice exercises are in the coursebook? Then moving through the stations with a book will be kind of pointless. Students may say, why can I not just stay in one table and go through the activities in one place?. (I tried this and some students complain about moving about too much around the classroom, they wanted to stay in one place!)
Thank you for your thoughts!
Nuria
HI Nuria,
Sorry for the late response (I did not receive a notification of your comment and just saw it).
So many great questions!
1) how do you manage with the feedback? // I give feedback as I monitor students’ work and, depending on the aqctivity, I collect certain tasks so I can check, sometimes grade and then give back with corrections or written feedback.
2) How are students checking their answers? Are you giving them an answer key? At what stage do they have acess to the answer key? // It depends on the objective of the station. Sometimes I give them an answer key within the station, which they must revise only when they have finished. Then I clarify when doubts arise.
3) What about if students follow a coursebook and the practice exercises are in the coursebook? I believe the stations with different resources and content materials. So if you use a coursebook, you could use it in one station, but it would be a good idea to vary with a worksheet, powerpoint, game, QR code, audio, hands-on creative activity, etc. depending on the topic and the objective of the station. You’re right, if it’s all just the book, then what’s the point?
Thanks for your comments and questions. Hope I have clarified your doubts. 🙂
Pingback: Thoughts on Flipping a Classroom | Digital Portfolio - Scott Leitzel
In an Indian context, this is working out very well. Your images and explanation were of great help. I used them for the reading classes of the tertiary level learners and it works wonderfully well.
Merlin, how great to know the extent to which my post has reached. I’m happy the activity worked well. How did you use it for reading class?
Pingback: Flipped learning – ‘In-class flipped’ – T&L Exchange